《数学分析选讲》课程教学大纲

课程编号：0712020217

课程基本情况：

1．课程名称：数学分析选讲

2．英文名称：Selected Topics on Mathematical Analysis

3．课程属性：专业选修课

4．学　　分： 4  总学时：68

5．适用专业：数学与应用数学，信息与计算科学、应用统计学

6．先修课程：数学分析、高等代数、解析几何、常微分方程等

7．考核形式：考查

一、本课程的性质、地位和作用

课程性质：本课程属于专业选修课．

课程的地位和意义：《数学分析选讲》是数学系数学与应用数学专业、信息与计算科学专业和应用统计学专业的一门提高性专业选修课．本课程主要是针对已修课程《数学分析》中的内容、方法、思想等作进一步补充和完善. 它对数学系高年级学生进一步学习和掌握《数学分析》中的内容、方法和思想等作出了更高层次的要求. 因此，为了强化学生已学知识，并对所学知识进行较系统的总结和分类指导，进一步培养学生运用数学分析方法解决问题的思维能力，提高学生的综合素质，开设该选修课程是必要的．

二、教学目的与要求

本课程的目的是通过对数学分析的知识结构、思想方法及解题方法等的进一步讲授，通过有针对性的习题讲解和演练，帮助学生复习和重新认识《数学分析》中的内容、方法和思想，使学生进一步提高分析问题和解决问题的能力，注重培养学生分析、探讨、发现、创新等能力．

本课程的教学要求是在《数学分析》教学大纲的教学要求基础上，着重选择重要的知识点进行讲解和演练，适当提高和强化相关知识点的教学要求.

三、课程教学内容及学时安排

按照教学方案安排，本课程安排在第7学期讲授，全学程共68学时，其中课内讲授46学时，习题课22学时，具体讲授内容及学时安排见下表：

数学分析选讲教学内容及学时分配表

四、参考教材与书目

1．参考教材

自编讲义

2．参考书目

1. 裴礼文．数学分析中的典型问题与方法（第二版）．北京：高等教育出版社，2006

2. Vladimir A. Zorich. Mathematical Analysis．Springer-Verlag, Berlin Heidelberg. 2004

    

第一讲 一元函数极限（8学时）

【教学目的与要求】

本章的教学目的是系统复习数列与函数极限的有关知识，概括总结证明极限和求极限的的各种方法。要求在较高的技巧和难度上综合讨论极限的两大基本问题-----证明极限的存在性和求极限．要求学生应首先复习教材的基本内容，注意各个求法的特点及适用范围．

具体要求是：

1. 正确理解极限、无穷小、上（下）确界、上（下）极限的概念与性质；

2. 熟练应用四则运算法则、两个重要极限、单调有界定理、两边夹定理、柯西收敛准则；

3. 正确理解Stolze定理，并能灵活应用；

4. 灵活应用求极限的若干方法．重点训练定义法、递推形式的极限求法、不定式极限的求法；

5. 掌握有关极限的证明方法； 利用极限的定义证明、利用单调有界定理证明、利用上（下）极限证明．

【教学重点】

函数极限与数列极限的计算和证明.

【教学难点】

上、下极限．

【教学方法】

讲授、讨论，多媒体。

【教学内容】

有关数列（函数）极限的基本概念与基本理论；数列收敛与发散的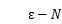定义、函数（单侧）极限的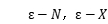定义、无穷小量的概念；收敛数列（正常函数极限）的存在性：单调有界原理、两边夹逼定理、柯西收敛准则；收敛数列（正常函数极限）的性质：唯一性、（局部）有界性、（局部）保号性、不等式性；求极限的四则运算法则，无穷小的性质，两个重要极限；几个关系：函数极限与数列极限、极限与单侧极限、极限与上下极限；Stolze定理；函数与数列上、下极限的三种等价描述、性质；概括习题类型及其求解方法；用定义证明极限的存在性；根据极限的定义与性质证明；求极限的若干方法：定义法、各种技巧恒等变形，利用四则运算法则、重要极限、无穷小的性质、单调有界定理、两边夹逼定理、柯西收敛准则、Stolze定理、利用导数（定积分）定义、归结原则、洛必达法则、泰勒公式、级数理论等．

第二讲 一元函数的连续（8学时）

【教学目的与要求】

本章的目的是复习函数的连续性、一致连续性的概念与性质，系统总结有关连续性及一致连续性的证明方法，归纳它们的性质及其应用，特别是闭区间上连续函数性质的应用．要求学生能正确理解概念，熟练掌握性质，灵活运用这些知识解决相关数学问题．

具体要求是：

1. 正确理解连续与一致连续的概念与性质、间断点的分类；

2. 熟练应用连续函数的性质进行证明；

3. 灵活应用零点存在定理；

4. 会用连续性解函数方程；

5. 掌握利用闭区间套定理、有限覆盖定理证明相关问题的核心思想， 理解构造闭区间套、开覆盖的方法．

【教学重点】

函数的连续性、一致连续性的性质及应用.

【教学难点】

一致连续性的证明及利用闭区间套定理、有限覆盖定理证明问题．

【教学方法】

讲授、讨论，多媒体.

【教学内容】

基本概念与基本理论，连续性概念，函数在一点（单侧）连续、在区间上连续的定义、间断点的定义及其分类，单侧连续与连续的关系，连续函数的局部性质（在一点连续）：有界性、保号性，运算法则——四则运算法则、反函数与复合函数的连续性，一致连续性的概念及性质；一致连续性与连续性的关系，闭区间上连续函数的（整体）性质：有界性、最值性、介值性、零点存在性、一致连续性，函数方程的讨论，实数连续性定理，概括习题类型及其求解方法，利用定义证明函数的一致连续性与不一致连续性，利用性质证题，用“零点存在定理”证明方程根的存在性，函数方程的求解，利用闭区间套定理、有限覆盖定理证明题．

第三讲 一元函数的微分学（10学时）

【教学目的与要求】

本章的教学目的与要求是系统复习一元函数导数、微分中值定理、泰勒公式及导数的应用，归纳总结有关知识点，阐述思想方法和解题基本思路，提高解题能力．重点讲解中值定理的应用技巧．要求学生树立正确的解题思想，注意从解题过程中体会相关的数学思想方法．

具体要求是：

1. 正确理解导数的概念，熟练掌握函数的求导法则；

2. 理解可导与可微、连续的关系；

3. 理解微分中值定理的实质，并能灵活运用它们证明等式与不等式；

4. 理解极限的定义、判别条件，能运用之解决实际中的最值问题；

5. 会利用单调性、极限、曲线的凹凸性证明不等式.

【教学重点】

重点是函数导数的概念、微分中值定理的应用.

【教学难点】

难点是熟练利用微分中值定理解题．

【教学方法】

讲授、讨论，多媒体.

【教学内容】

基本概念和基本理论，函数在一点的单（双）侧导数、函数在区间上的导数、高阶导数的定义，导数的几何意义，求导法则、四则运算、反函数的导数、复合函数的导数、参量方程所表示的函数的导数、隐函数的导数，几个关系：可导与连续的关系，导数与左右导数的关系，可导与可微的关系，微分中值定理：费马定理、罗尔定理、拉格朗日中值定理、柯西中值定理、泰勒公式，导数与函数单调性的关系，极值的定义；取极值的必要条件、充分条件，曲线的凹凸性定义、判别方法，概括习题类型及其求解方法：求各类函数的低阶导数，方法——定义法、求导法则；高阶导数的求法——拆项法、莱布尼兹公式、数学归纳法、递推公式法、利用泰勒公式，利用微分中值定理证明题：证明恒等式、证明不等式，证明零点的存在、唯一性，导数的中值估计、界的估计、求无穷远处的极限、中值的极限，极值、最值、函数的单调性、曲线的凹凸性讨论．

第四讲 一元函数积分学（8学时）

【教学目的与要求】

本章的目的与要求是复习如下几方面内容：积分与极限，可积性，定积分的性质，积分值的估计，积分等式与不等式的证明，积分学基本定理，几个重要不等式及应用，非正常积分等．系统总结与积分有关的证明方法，要求学生能正确理解概念，熟练掌握性质，理解证明方法的实质，提高解题能力．

具体要求是：

1. 牢记定积分的性质，特别是不等式性与中值定理；

2. 正确理解可积性的第一、第二充要条件并能运用之证明可积性；

3. 理解微积分学基本定理，熟练应用它进行一些证明题；

4. 领会非正常积分敛散性、绝对收敛、条件收敛的定义；

5. 熟练应用比较收敛法、阿贝尔判敛法、狄利克雷判敛法．

【教学重点】

定积分的性质、微积分学基本定理的使用.

【教学难点】

非正常积分敛散性的判断．

【教学方法】

讲授、讨论，多媒体.

【教学内容】

基本概念和基本理论，定积分的性质：线性性、可加性、不等式性、中值定理，可积性定理（充要条件），可积函数类，变限积分的函数的连续性、可导性．微积分学基本定理，定积分存在与原函数存在的关系，非正常积分的敛散性、绝对收敛、条件收敛的定义、判别法，概括习题类型及其求解方法：研究积分的存在性方法——定义法、定理法；积分的极限计算——利用定积分的定义、性质，重点讲拟合法，用微积分学基本定理处理的几类问题：求导法、求极限，研究连续函数的原函数的性质——奇偶性、最值性、有界性、极限的存在性等，证明积分不等式方法——作变限积分辅助函数、定积分的不等式性质、换元法、微分（积分）中值定理、泰勒公式、一些重要不等式，非正常积分的计算：变量替换、分部积分、牛—-莱公式，非正常积分的敛散性的判定：定义法、运算性质、比较法部分和有界法、阿贝尔法、狄利克雷法、柯西准则、用分部积分法或变量替换转化其形式，非正常积分的极限、无穷限非正常积分的敛散性与无穷远处极限的状态的讨论．

第五讲 级数（10学时）

【教学目的与要求】

本章的目的是复习如下几方面内容：数项级数的性质、正项级数的敛散性的判别法、任意项级数敛散性的判别法、函数列与函数项级数一致收敛性的判别法、极限（和）函数的性质、幂级数的收敛域与和函数的计算．系统总结级数理论，理解各判别法实质．特别是函数项级数一致收敛性与和函数的解析性质．要求学生能正确理解概念，熟练掌握各判敛法．培养学生建立正确的数学思维和解题能力．

具体要求是：

1. 正确理解数项级数的性质，掌握正项级数的各种收敛判别法．

2. 正确理解函数列与函数项级数的收敛域及一致收敛、非一致收敛的概念．

3. 掌握函数列与函数项级数一致收敛的各种判别法，注意其实用范围．能用它们正确判别函数列与函数项级数的一致收敛、非一致收敛．

4. 理解函数列与函数项级数的极限函数（和函数）的性质，并运用之．

5. 掌握幂级数收敛的阿贝尔定理，会求幂级数的收敛域．

【教学重点】

判断数项级数的敛散性，函数列（函数项级数）一致收敛判别，幂级数收敛域的确定。

【教学难点】

难点是函数列（函数项级数）一致收敛判别．

【教学方法】

讲授、讨论，多媒体.

【教学内容】

基本概念和基本理论，数列与函数项级数的有关概念：部分和函数、极限（和）函数、点点收敛、一致收敛，收敛级数的的性质：线性性、改变有限项性、加括号法则、必要条件，比较判别法与极限形式，比式与根式判别法与极限形式，莱布尼兹判别法，阿贝尔、狄利克雷判敛法，函数列（函数项级数）一致收敛判别：柯西准则、确界充要条件、狄尼定理、M判别法、阿贝尔法、狄利克雷法，一致收敛函数列（函数项级数）的性质：连续性、（逐项）求积、（逐项）求导，幂级数收敛的阿贝尔定理．幂级数收敛的一致收敛性，概括习题类型及其求解方法：判别正项级数的敛散性——定义法、判阶法、比较法、部分和有界、比式与根式法及极限形式、积分法；判别任意项级数的敛散性——用正项级数的判别法判断绝对收敛；用收敛的定义、性质、莱布尼兹判别法、阿贝尔、狄利克雷判敛法判断条件收敛；根据收敛级数的概念与性质证明，级数求和方法：定义法、利用线性性质、构造幂级数利用逐项求积、逐项求导定理，判断函数列一致收敛性与非一致收敛性——根据定义、柯西准则、确界充要条件、狄尼定理，判断函数项级数一致收敛性与非一致收敛性——根据定义、柯西准则、确界充要条件、狄尼定理、M判别法、阿贝尔法、狄利克雷法，利用一致收敛的性质证题，求函数项级数、幂级数的收敛域：根据正项级数的比式与根式判别法、求收敛半径方法，求幂级数和函数的间接方法：用变量替换、线性性、逐项求积、逐项求导定理．

第六讲 多元函数微分学（8学时）

【教学目的与要求】

本章的目的是系统复习多元函数微分学的基本知识，通过概括总结本部分的内容，使学生们能理解相关的基本概念与基本定理，认识一元与多元函数相应内容的异同点，从而加深对基本理论的理解，达到提高学生分析问题解决问题的能力，培养思维的深刻性．

具体要求是：

1. 正确理解多元函数的极限的概念，掌握证明二重极限不存在性的方法．

2. 正确理解多元函数的连续、偏导数、全微分、方向导数的概念，并比较它们与一元函数相应概念的异同，搞清连续、偏导数存在、可微、方向导数存在之间的关系．

3. 理解多元复合函数与隐函数（组）的微分法，熟练计算多元函数（复合函数、隐函数）的偏导数、全微分．会求方向导数．

【教学重点】

多元复合函数、隐函数（组）的微分法。

【教学难点】

难点是分段函数可微性的讨论．

【教学方法】

讲授、讨论，多媒体.

【教学内容】

基本概念和基本理论，多元函数的极限、连续、偏导数、全微分、方向导数的概念，多元函数极值、条件极值的概念，二重极限与累次极限的关系，二元函数的连续、偏导数、全微分之间的关系，多元复合函数、隐函数（组）的偏导数、全微分的计算，对微分方程作变量替换化简方程，多元分段函数可微性的研究．

第七讲 重积分（4学时）

【教学目的与要求】

本章的目的与要求是系统复习二（三）重积分的概念、性质、计算方法及含参量变量正常积分的概念与性质．重点补充介绍利用对称性计算重积分的简便方法．通过总结这些方法，使学生加深理解相应的知识，熟悉各种求积分的方法，从而达到提高运算能力的目的．

具体要求是：

1. 正确理解含参变量积分的概念与性质．会应用性质定理讨论含参变量积分定义的函数的连续性、可导性．

2. 熟练应用变量替换、对称性计算二（三）重积分．

【教学重点】

重积分的计算.

【教学难点】

重积分化为累次积分限的确定及含参量变量正常积分的性质的使用．

【教学方法】

讲授、讨论，多媒体.

【教学内容】

基本概念和基本理论：

二（三）重积分的概念、性质，二重积分的计算，二重积分的一般变换，三重积分的计算与变量替换（区域对称性、轮换对称性），含参量正常积分的概念、性质.

概括习题类型及其求解方法：

二（三）重积分的计算——在直角坐标系、极坐标系、柱面坐标系、球面坐标系下化为累次积分计算；利用一般变量替换、对称性计算，利用二重积分求二元函数的偏导数，利用二重积分证明等式与不等式，计算含参变量积分——直接计算法、间接计算法，计算极限或讨论连续性、计算导数或讨论可导性——定义法、定理法，根据性质定理证题．

第八讲 曲线、曲面积分（4学时）

【教学目的与要求】

本章的目的是系统复习两类曲线、曲面积分的基本知识，通过概括总结本部分的内容，补充利用对称性计算这四种积分，使学生们能理解相关的基本概念与各种积分的计算方法，从而加深对基本理论的理解，达到提高学生分析问题解决问题的能力，培养思维的深刻性．

具体要求是：

1. 正确理解第一、第二型曲线（曲面）的定义、几何意义，理解两种曲线（曲面）积分间的关系．

2. 熟练掌握各种积分的直接计算方法，理解并灵活运用格林公式、高斯公式、斯托克斯公式计算线面积分．

3. 正确理解第二型平面（空间）曲线积分与路径无关的充要条件，利用它求原函数．

【教学重点】

计算两类线面积分，三个公式的使用.

【教学难点】

难点是第二型曲面积分的计算．

【教学方法】

讲授、讨论，多媒体.

【教学内容】

基本概念和基本理论：第一、第二型曲线（曲面）的定义、几何意义，两种曲线（曲面）积分间的关系，各种曲线（曲面）积分的直接计算法，格林公式、高斯公式、斯托克斯公式，第二型曲线积分与路径无关的充要条件。

概括习题类型及求解方法：第一型曲线（曲面）积分的计算：直接化为定积分、二重积分计算，利用积分区域的对称性计算，第二型曲线积分的计算：直接化为定积分、利用格林公式、曲线积分与路径无关性间接计算平面第二型曲线积分，利用斯托克斯公式计算空间第二型曲线积分，化为第一型曲线积分计算，第二型曲面积分的计算：直接化为二重积分计算、利用高斯公式间接计算，化为第一型曲面积分计算．

执笔人：王春 审定人：王春